自建Ｃ＃機器學習核心

這篇心得是應之前python spark decision tree 的老師Mercel Wang邀約所寫的，不過我也不清楚怎麼寫才適合，所以就先交待一下那門課的狀況吧．當時他是在FB的python Taiwan開了一個關於spark和決策樹的討論串，我當時剛好也好奇machine learning到底在幹嘛，就跟著討論串+1．

這門課以交作業的方式進行，當有人貼出該次作業後，就繼續發放下一週的作業，前幾個禮拜都要搜集和消化不少資料和文獻，不過好處是如果不知道作業怎麼寫，也能參考其他先做出來的人的作品，這門課對上班族來說負擔不算輕，得在下班和假日處理作業的事情，不過也因此從完全不知道ML是什麼東西的人，變成能夠講述ML大概是怎樣的東西．

不過我比較沒定力，從作業9之後，就沒再繼續了，一個是老師沒繼續出作業就懶得繼續下去，另一個是工作和生活上碰不到需要Hadoop的情境，加上hadoop/spark/scala的版本真是一團亂，所以一整個發懶．時間推移到今年三月，我在公司建構機聯網，蓋到一半突然想到用ML來判斷製程的參數到底好或壞，也許是好玩又可行的案子，因此又重新把之前看過的文獻和資料找了出來．

本來我是想說用現成的lib就好，但是沒想到公司的網路完全把python lib wheel擋起來，我又很懶得研究如何翻牆，於是就想說來看看這些lib的原始碼怎麼寫的好了～原本不看還好，看過才發現，「我根本看不懂他們在寫啥...」想說這樣不行，這樣根本寫不出東西呀！

我想了想，決定還是用最笨的方法好了，從數學方法一步步來蓋自己看得懂的ＭＬ（反正工控和製程的數據壓根稱不上“大”數據，一天有個2ＧB就不錯了，因此效率就不是我的首要考量），由於在工業控制和機械領域，C#是王道（c/c++是大神級玩的，小的玩不起），所以就以C#來撰寫，首先是以類神經網路開刀，花了個半天寫了個最初級的感知器，就覺得其實也不難嘛～哈哈！我就串了十幾個一樣的感知器來跑iris data來玩，感覺還ok．隔天就來挑戰SVM．結果發現我想得太單純了，這個有夠難懂．

SVM網路的資料非常非常非常非常的多，但是能夠把數學方法解釋得詳細的沒幾個，甚是錯誤不少，比如說向量和純量的表示法搞錯，符號定義不明，亂用之類的（暈）．暈了幾天後，總算找到一個非常淺顯易懂的教材，MIT的machine learning課程[1]，用它教學的步驟總算把一個可以二分類的SVM蓋起來了，分類的邏輯搞定，但是需要大量的矩陣運算，因此在一個禮拜內惡補了不少線性代數的東西（以前只有大二修過工程數學，有講到半個學期的線代，但早還給教授了，畢竟她研究有需要用到，她要用的時候沒有會很困擾的），總算蓋了一個高斯消去運算器來處理矩陣，不過實際跑的時候發現，遇到[20*20]以上的矩陣就爆炸了．後來找了找其他替代方案，找到了一個叫做SMO的演算法[2]，他是使用軼代法的方式來代替掉大量的矩陣運算，並能夠保證運算的正確性，看到這個的時候，覺得發明這個的人根本是天才！後來我採用的方式是簡易版的SMO[3]，在演算法上比原本論文寫得更好懂，超推薦！把SMO寫好後，實際跑的感覺超棒的，it works!（拿iris data試跑有90%up準確率）而且沒想到整個演算法也才不到300行，心情超好．

經過SVM的摧殘後，寫決策樹就輕鬆多了，只要補好統計學的基礎知識，像是binominal distribution，就能寫出一個C4.5的node，但後來發現決策樹在決定像double/float型別的資料上範圍，沒這麼好用（主要是我文獻和資料的搜集還不夠多，目前看到的範例都是字串資料當教材），所以目前就只拿它來玩字串資料的分類了，像是分類MES上面的資料．

目前是把SVM拿來推論新增的製程參數的好壞，不過由於累積的樣本數還不夠多，所以還沒有一個明顯趨勢出現．也許根本沒趨勢也有可能，或是資料量大起來後發現自己寫的是錯的也難說．

沒想到當初無心參與python spark課程，找過的資料以及學到的ＭＬ知識，會真的應用到我工作的領域上，無心插柳呀．算是一個奇特的經驗，在這跟大家分享～哈．

參考資料
[1]https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-034-artificial-intelligence-fall-2010/tutorials/MIT6_034F10_tutor05.pdf
[2]http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.43.4376&rep=rep1&type=pdf
[3]http://cs229.stanford.edu/materials/smo.pdf

Control Beckhoff I/O module by C#

This method can directly control I/O module without PLC.
1. Install TwinCAD3
2. Refer the Library of Beckhoff

using TwinCAT.Ads;

3.declare the client object and output array
private TwinCAT.Ads.TcAdsClient client; UInt32[][] OUTPUTs = new UInt32[16][];

4. Using connect method of client object
client.Connect(11);

5. the data structure of IO array: assume there are 16 output ports, then the length of array is 16. Each port has 2 elements, both data type of elements are Uint 32. The first element is the practical address of IO module, the second element is the virtual address of the port. For instance, if the virtual address of output port 1 is 0xC10000D0, then output port 2 is 0xC10000D0+(Uint32)1=0xC10000D1.

6.As we acquire the practical address and virtual address of IO module and its ports. we can use

client.WriteAny(master_address,IO_address,bool);

to control output ports directly.

Or

client.ReadAny(master_address,IO_address, typeof(var));

to read the current state of ports.

the sample code is as below:

for (int i = 0; i < OUTPUTs.Length; i++)
            {
                OUTPUTs[i] = new UInt32[2];
                OUTPUTs[i][0] = 0x3040030;
                OUTPUTs[i][1] = 0xC10000D0 + (UInt32)i;



                object c = client.ReadAny(OUTPUTs[i][0], OUTPUTs[i][1], typeof(byte));
                if ((byte)c == 1)
                {
                    client.WriteAny(OUTPUTs[i][0], OUTPUTs[i][1], (bool)false);
                    rds[i].Checked = false;//radio button object
                    cbs[i].Checked = false;//check box object
                }
                else
                {

                    client.WriteAny(OUTPUTs[i][0], OUTPUTs[i][1], (bool)true);
                    rds[i].Checked = true;
                    cbs[i].Checked = true;
                }
                listBox1.Items.Add(c);

傾斜度 Angularity

傾斜度 Angularity
＃以下圖是用keynote畫出來的，所以並不完全符合工程規範，單純適意用
傾斜度本來是想翻成角度度，但聽起來又很奇怪，後來看到一本書是寫傾斜度，那就這樣用囉．
傾斜度是說，以一個面當基準時，和它有夾角的傾斜面的起伏程度．
傾斜度的符號如圖一

圖一

在工程圖上的範例如圖二

圖二

一般就筆者的經驗，即使是工程人員，不少也會以為說這個公差的讀法是70+-0.3度，但實際上，如果照角度公差來配的話，會在組裝和製造上弄出非常大的問題．

因此，該公差的讀法是，在以Ａ基準為零點，該面和Ａ基準之夾角為70度，而該面有上下0.3的帶狀公差，如圖三所示．

圖三

以上為傾斜度之簡介

正位度之二-考量材料條件

考量材料條件的正位度
在講這之前，得先說明什麼是材料條件，一般來說我們會在工程圖上的位置公差上看到下面兩個符號(圖一)：

圖一

Ｍ代表最大材料條件/邊界(Maximum Material Condition/Boundary)，在實心特徵（如插銷，boss, pin...）上就代表取其最大值，在空心特徵(如孔)則是取其最小值，以保證工件的材料是在最多的狀況．

Ｌ代表最少材料條件/邊界(Least Material Condition/Boundary)，在實心特徵（如插銷，boss, pin...）上就代表取其最小值，在空心特徵(如孔)則是取其最大值，以保證工件的材料是在最少的狀況．

考量材料狀況的正位度並不是說把目標的孔或是柱體做到最大或者最少材料，而是以最大或最小材料狀況作為參考標準，去變動公差範圍．

參考材料狀況的正位度標註如圖二

圖二

在正位度公差後面標注材料條件符號

以一個例子來講解有材料條件的正位度，見圖三

圖三

該範例是一個鈑件上面有一個孔，在正位度標明最大材料條件的前提下，此公差的解讀方式為“在孔的直徑最小的情況下(19.8)，有直徑0.2的公差帶，當孔的直徑變大時，其公差帶也會隨之增加"，其公差帶如表一

表一

用圖來解釋，則如圖四和圖五

圖四

圖五

在這種情況下，孔的半徑越大，可擁有的公差帶就越大，這個是考量材料條件的正位度特別之處．這種公差設計可以減少在製造過程中機器或人所造成的加工誤差所造成的組裝困難，並減少加工之成本和困難度．

至於最小材料條件也是相同的概念，以圖六為例

圖六

以最少材料條件為基準，即以直徑20.2的時候，有正位度公差帶直徑0.2，之後孔徑越小，所擁有的正位度公差就越大，如表二所示

表二

以圖來表示，及圖七和圖八

圖七

圖八

在這種情況下，孔越小，所擁有的公差帶越大，一般來說，最小材料條件的正位度公差比較少用在孔上，以組裝的觀點來說較不符合需求，但還是得看工件設計和製造上的需求來選擇適合的公差分配方法，沒有絕對．

正位度 True Position

正位度(TRUE POSITION)

正位度在幾何公差上的定義（作者自己的定義）是標明一個特徵（通常是圓柱狀物體或圓柱狀孔位）的位置之容許公差帶，和一般的公差表示法有所不同，一般常見的尺寸公差(圖一）

圖一

其可變動範圍長寬各為+-0.2，所以他的公差帶會是一個矩形，見圖二

圖二

公差帶的交集就是一個長0.4寬0.4矩形

至於正位度，它的公差帶是圓形的，這個是和普通的尺寸公差最大差別．

正位度的符號如圖三

圖三

由於正位度必須有參考的基準特徵(比如說基準面，基準軸，基準輪廓...)，因此其標注方式通常如圖四

圖四

其意義為 所標註的圓柱狀特徵，以Ａ基準當作參考的前提下，該特徵和Ａ基準間的位置可以有直徑0.02的公差帶．

以一個實際例子來說，如圖五

圖五

圖五為一個版件上有一圓孔，該圓孔的直徑可介於19.9~20.1之間，而其正位度的解讀方式為，“不管該圓孔目前的直徑為多少，只要介於19.9~20.1之間，以Ａ基準算過去50的長度，Ｂ基準算過去40的長度為圓心，實際加工出來的圓孔的圓心和基準對出來的圓心可以有直徑0.02的公差帶．如圖六所示，

圖六

至於為什麼要定義正位度這種公差呢？主要是為了組裝的設計需求而生，當今天有一整組孔要卡在一整組相對應圓柱體上，使用正位度公差比一般尺寸公差容易在製程上容易控制其尺寸和配合條件，當然這得配合上最大材料或最小材料條件的正位度公差，這個在下一篇會詳細說明．大致上正位度的入門就是這樣．

Laser Tracker (02)-量測實務

日前有介紹過，對於60英呎(約1.5公尺)的鋁製棒材，有0.2度C的溫差時會有大概7um的熱膨脹長度差異，當雷射追蹤儀需要量測的物件都是非常大的(像747-400的機身長度有71公尺)，而且現場並無法進行溫控，所以溫度差異造成的尺寸誤差是非常可觀的。因此在量測物件之前，就得先量測物件本身的溫度，確定物件本身的溫度為何~通常物件的設計人員會規定至少一個物件要取多少個溫度樣本，在物件的哪幾個地方取溫度樣本，同一時間的溫度樣本的差異不可超過幾度，每隔多少時間要取樣...等限制條件，跟CMM在恆溫條件(20度C+/-1度C)量測比起來，雷射追蹤儀需要注意更多外在因素，溫度就是其中一樣。

有了溫度和尺寸差異的問題後，為了解決這個問題，設計人員會訂定ㄧ個標準溫度(比如說20度C)，並以標準溫度時的尺寸當做標稱尺寸(Nominal dimension)，並以scale bar(我翻做比例尺棒)當做驗算標準，假定今天我在物件平均溫度為25度C時量測了所有尺寸，這些尺寸數據很明顯不可能和標稱尺寸(標稱為20度C)吻合，甚至無法達成公差要求。此時便需要把所有量測數據做Best Fit Transformation(最佳擬何轉換)，轉換的矩陣就和機構學上的正向運動學的座標轉換矩陣類似，有空會再補ㄧ篇數學上的詳細計算~ 經過最佳擬何轉換後，量測數據和標稱尺寸的差異就會小很多，比例也會有所縮放(通常機器人學的關節運算或是CMM的疊代運算是不牽涉比例縮放的)，因此會有個縮放前和縮放後的比值，我翻譯成比例因數(scale factor)，但要如何保證轉換後的量測數據是可信的，此時就得靠比例尺棒了。

比例尺棒必須和物件的材料一致或熱膨脹係數相近，才有辦法驗證轉換的數據可信度。在量測物件溫度後，會再量測比例尺棒的溫度，先確保兩者溫度相近，在量測完物件的尺寸後，會再量測比例尺棒的長度，這比例尺棒的長度並不會參加最佳擬何轉換，而是我們轉換完後，會把比例尺棒的長度乘上比例因數來看比例尺棒的縮放長度是否和其標稱長度一致，如果在公差範圍內就代表轉換的結果是可信的。

這一篇就先寫到這，下一篇還是寫量測實務，因為使用這個儀器要注意的點真的一大堆

熱膨脹對長度的影響

最近用CMM量長度60 inch的鋁製棒材時發現了一個有趣的效應，當時量測室的溫度是19.3度C，然後棒材的溫度是19.5度C (從室溫27度放在量測室ㄧ個下午後的溫度)，上CMM量測頭尾端重複5次，過程大約10分鐘，出來的結果是逐步縮小的，每次的結果都會很剛好的縮短0.0002 inch~0.0003 inch(約5-8um)，後來計算了一下溫度差異即使在只有0.2度C的情況，會造成的熱膨脹差異總共會有:

鋁熱膨脹係數: 23.2 x 10e-6 /度C

鋁材長度: 60 inch*25.4 mm/inch=1524 mm

溫度差 0.2度C

總共會造成的差異為:

長度差=23.2*10e-6*1524*0.2=0.07007 mm =7.07um

所以即使在溫差很小(0.2度C)的情況，在中大型工件所造成的長度差異(7um)也是會讓工件超過公差的~~~

(如果配合熱傳導計算就能差不多能模擬每分鐘的溫度變化和長度變化了~~)

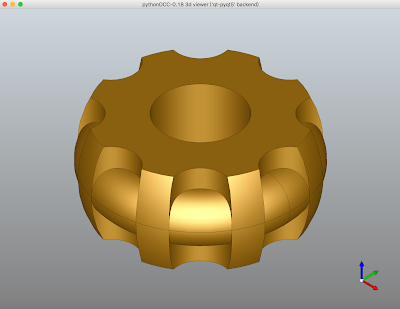
PythonOCC 使用心得

pythonOCC是個非常好用的工具，它就是把OpenCasCade包成python的library，基本上商用CAD/CAM軟體做得到的事情，它都能做到，加上它把QT也一起整合起來，因此使用和開發上是個很方便的工具，尤其是特殊客製化的功能上．

圖一 PythonOCC的繪圖介面

雷射追蹤儀(LASER TRACKER)簡介之二

由於雷射追蹤儀是移動式座標量測儀器，因此該儀器非常容易受到外在環境影響，所以在使用前都需做場檢查(Field Check)．場檢查是為了確保環境的變因在量測可接受範圍內，通常要做的項目有： 溫度監測 場地穩定度檢查 雷射追蹤儀角度檢查 ADM/IFM檢查，一套完整的檢查搞下來大約1～2小時，是個耗時費工的檢查儀器．