傾斜度 Angularity

傾斜度 Angularity
＃以下圖是用keynote畫出來的，所以並不完全符合工程規範，單純適意用
傾斜度本來是想翻成角度度，但聽起來又很奇怪，後來看到一本書是寫傾斜度，那就這樣用囉．
傾斜度是說，以一個面當基準時，和它有夾角的傾斜面的起伏程度．
傾斜度的符號如圖一

圖一

在工程圖上的範例如圖二

圖二

一般就筆者的經驗，即使是工程人員，不少也會以為說這個公差的讀法是70+-0.3度，但實際上，如果照角度公差來配的話，會在組裝和製造上弄出非常大的問題．

因此，該公差的讀法是，在以Ａ基準為零點，該面和Ａ基準之夾角為70度，而該面有上下0.3的帶狀公差，如圖三所示．

圖三

以上為傾斜度之簡介

正位度之二-考量材料條件

考量材料條件的正位度
在講這之前，得先說明什麼是材料條件，一般來說我們會在工程圖上的位置公差上看到下面兩個符號(圖一)：

圖一

Ｍ代表最大材料條件/邊界(Maximum Material Condition/Boundary)，在實心特徵（如插銷，boss, pin...）上就代表取其最大值，在空心特徵(如孔)則是取其最小值，以保證工件的材料是在最多的狀況．

Ｌ代表最少材料條件/邊界(Least Material Condition/Boundary)，在實心特徵（如插銷，boss, pin...）上就代表取其最小值，在空心特徵(如孔)則是取其最大值，以保證工件的材料是在最少的狀況．

考量材料狀況的正位度並不是說把目標的孔或是柱體做到最大或者最少材料，而是以最大或最小材料狀況作為參考標準，去變動公差範圍．

參考材料狀況的正位度標註如圖二

圖二

在正位度公差後面標注材料條件符號

以一個例子來講解有材料條件的正位度，見圖三

圖三

該範例是一個鈑件上面有一個孔，在正位度標明最大材料條件的前提下，此公差的解讀方式為“在孔的直徑最小的情況下(19.8)，有直徑0.2的公差帶，當孔的直徑變大時，其公差帶也會隨之增加"，其公差帶如表一

表一

用圖來解釋，則如圖四和圖五

圖四

圖五

在這種情況下，孔的半徑越大，可擁有的公差帶就越大，這個是考量材料條件的正位度特別之處．這種公差設計可以減少在製造過程中機器或人所造成的加工誤差所造成的組裝困難，並減少加工之成本和困難度．

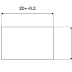
至於最小材料條件也是相同的概念，以圖六為例

圖六

以最少材料條件為基準，即以直徑20.2的時候，有正位度公差帶直徑0.2，之後孔徑越小，所擁有的正位度公差就越大，如表二所示

表二

以圖來表示，及圖七和圖八

圖七

圖八

在這種情況下，孔越小，所擁有的公差帶越大，一般來說，最小材料條件的正位度公差比較少用在孔上，以組裝的觀點來說較不符合需求，但還是得看工件設計和製造上的需求來選擇適合的公差分配方法，沒有絕對．

正位度 True Position

正位度(TRUE POSITION)

正位度在幾何公差上的定義（作者自己的定義）是標明一個特徵（通常是圓柱狀物體或圓柱狀孔位）的位置之容許公差帶，和一般的公差表示法有所不同，一般常見的尺寸公差(圖一）

圖一

其可變動範圍長寬各為+-0.2，所以他的公差帶會是一個矩形，見圖二

圖二

公差帶的交集就是一個長0.4寬0.4矩形

至於正位度，它的公差帶是圓形的，這個是和普通的尺寸公差最大差別．

正位度的符號如圖三

圖三

由於正位度必須有參考的基準特徵(比如說基準面，基準軸，基準輪廓...)，因此其標注方式通常如圖四

圖四

其意義為 所標註的圓柱狀特徵，以Ａ基準當作參考的前提下，該特徵和Ａ基準間的位置可以有直徑0.02的公差帶．

以一個實際例子來說，如圖五

圖五

圖五為一個版件上有一圓孔，該圓孔的直徑可介於19.9~20.1之間，而其正位度的解讀方式為，“不管該圓孔目前的直徑為多少，只要介於19.9~20.1之間，以Ａ基準算過去50的長度，Ｂ基準算過去40的長度為圓心，實際加工出來的圓孔的圓心和基準對出來的圓心可以有直徑0.02的公差帶．如圖六所示，

圖六

至於為什麼要定義正位度這種公差呢？主要是為了組裝的設計需求而生，當今天有一整組孔要卡在一整組相對應圓柱體上，使用正位度公差比一般尺寸公差容易在製程上容易控制其尺寸和配合條件，當然這得配合上最大材料或最小材料條件的正位度公差，這個在下一篇會詳細說明．大致上正位度的入門就是這樣．

Laser Tracker (02)-量測實務

日前有介紹過，對於60英呎(約1.5公尺)的鋁製棒材，有0.2度C的溫差時會有大概7um的熱膨脹長度差異，當雷射追蹤儀需要量測的物件都是非常大的(像747-400的機身長度有71公尺)，而且現場並無法進行溫控，所以溫度差異造成的尺寸誤差是非常可觀的。因此在量測物件之前，就得先量測物件本身的溫度，確定物件本身的溫度為何~通常物件的設計人員會規定至少一個物件要取多少個溫度樣本，在物件的哪幾個地方取溫度樣本，同一時間的溫度樣本的差異不可超過幾度，每隔多少時間要取樣...等限制條件，跟CMM在恆溫條件(20度C+/-1度C)量測比起來，雷射追蹤儀需要注意更多外在因素，溫度就是其中一樣。

有了溫度和尺寸差異的問題後，為了解決這個問題，設計人員會訂定ㄧ個標準溫度(比如說20度C)，並以標準溫度時的尺寸當做標稱尺寸(Nominal dimension)，並以scale bar(我翻做比例尺棒)當做驗算標準，假定今天我在物件平均溫度為25度C時量測了所有尺寸，這些尺寸數據很明顯不可能和標稱尺寸(標稱為20度C)吻合，甚至無法達成公差要求。此時便需要把所有量測數據做Best Fit Transformation(最佳擬何轉換)，轉換的矩陣就和機構學上的正向運動學的座標轉換矩陣類似，有空會再補ㄧ篇數學上的詳細計算~ 經過最佳擬何轉換後，量測數據和標稱尺寸的差異就會小很多，比例也會有所縮放(通常機器人學的關節運算或是CMM的疊代運算是不牽涉比例縮放的)，因此會有個縮放前和縮放後的比值，我翻譯成比例因數(scale factor)，但要如何保證轉換後的量測數據是可信的，此時就得靠比例尺棒了。

比例尺棒必須和物件的材料一致或熱膨脹係數相近，才有辦法驗證轉換的數據可信度。在量測物件溫度後，會再量測比例尺棒的溫度，先確保兩者溫度相近，在量測完物件的尺寸後，會再量測比例尺棒的長度，這比例尺棒的長度並不會參加最佳擬何轉換，而是我們轉換完後，會把比例尺棒的長度乘上比例因數來看比例尺棒的縮放長度是否和其標稱長度一致，如果在公差範圍內就代表轉換的結果是可信的。

這一篇就先寫到這，下一篇還是寫量測實務，因為使用這個儀器要注意的點真的一大堆

熱膨脹對長度的影響

最近用CMM量長度60 inch的鋁製棒材時發現了一個有趣的效應，當時量測室的溫度是19.3度C，然後棒材的溫度是19.5度C (從室溫27度放在量測室ㄧ個下午後的溫度)，上CMM量測頭尾端重複5次，過程大約10分鐘，出來的結果是逐步縮小的，每次的結果都會很剛好的縮短0.0002 inch~0.0003 inch(約5-8um)，後來計算了一下溫度差異即使在只有0.2度C的情況，會造成的熱膨脹差異總共會有:

鋁熱膨脹係數: 23.2 x 10e-6 /度C

鋁材長度: 60 inch*25.4 mm/inch=1524 mm

溫度差 0.2度C

總共會造成的差異為:

長度差=23.2*10e-6*1524*0.2=0.07007 mm =7.07um

所以即使在溫差很小(0.2度C)的情況，在中大型工件所造成的長度差異(7um)也是會讓工件超過公差的~~~

(如果配合熱傳導計算就能差不多能模擬每分鐘的溫度變化和長度變化了~~)